Mängileer

D Mängi as gedankligi Zämmefassig vo Objekt

D Mängileer isch e Däilgebiet vo dr Mathematik, wo Mängene vo Objekt studiert. Jeedi Art vo Objekt cha zwar zun ere Mängi zämmegfasst wärde, aber d Mängileer wird am hüfigste aagwändet bi Objekt, wo für d Mathematik relewant si.

D Bedütig vo dr Mängileer

D Mängileer isch hützudags das grundlegende Däilgebiet vo dr Mathematik, wil mä hüte die ganzi Mathematik üübligerwiis in dr Sprooch vo dr Mängileer formuliert und sä uf de Axiom vo dr Mängileer ufbaut. Die mäiste mathematische Objekt, wo in Däilberiich wie under anderem Algebra, Analysis, Geometrii, Stochastik oder Topologii behandlet wärde, löön sich as Mängene definiere. Für dass d Mängileer e son e wichdigi Wüsseschaft isch, isch si no rächt jung. Erst wo d Grundlaagekriise vo dr Mathematik am Aafang vom 20. Joorhundert überwunde worde isch, het d Mängileer dr zentral und grundlegendi Blatz in dr Mathematik afo iinee, wo si hüte het.

Mächdikäit

Für ändligi Mängene isch d Mächdigkäit gliich wie d Zaal vo de Elimänt vo dr Mängi, das isch äntwääder e natürligi Zaal oder Null.

Bi unändlige Mängene definiert mä Ekwiwalänzklasse, wo die verschiidene Mängene drzueghööre und git dene Kardinalzaale $\aleph _{i}$. Äi Klass isch d Klass vo de abzellbare (mä säit au abzellbar unändlige) Mängene, wo alli gliich mächdig si wie d Mängi vo de natürlige Zaale $\mathbb {N}$. Doodrzue ghööre under anderem die ganze und die razionale Zaale.

Sümbol, wo in dr Mängileer brucht wärde

Für Mängene brucht mä im Allgemäine Groossbuechstaabe ($A,B,C...$) und für Elimänt vo Mängene Chliibuechstaabe ($a,b,c...$).

Definizionszäiche

Sümbol	Verwändig	Interpretazion
$:$	$A:B$	$A$ wird dur $B$ definiert
	$A:=B$	$A$ wird per Definizion gliich $B$ gsetzt
	$A:\Leftrightarrow B$	$A$ wird per Definizion gliichwärtig zu $B$ gsetzt

Mängikonstrukzion

Sümbol	Verwändig	Interpretazion
$\varnothing$		leeri Mängi
$\{~\}$	$\{a,b,\ldots \}$	D Mängi, wo us de Elimänt $a$, $b$ und so witer bestoot
$\mid$	$\{a\mid T(a)\}$	D Mängi vo de Elimänt $a$, wo d Bedingig $T(a)$ erfülle
$\colon$	$\{a\,\colon T(a)\}$

Mängioperazione

Sümbol	Verwändig	Interpretazion
$\cup$	$A\cup B$	Veräinigung vo de Mänge $A$ und $B$
$\cap$	$A\cap B$	Durchschnitt vo de Mänge $A$ und $B$
$\setminus$	$A\setminus B$	Differänz vo de Mänge $A$ und $B$
$\triangle$	$A\,\triangle \,B$	symmetrischi Differänz vo de Mänge $A$ und $B$
$\times$	$A\times B$	kartesischs Brodukt vo de Mänge $A$ und $B$
${\dot {\cup }}$	$A\,{\dot {\cup }}\,B$	Veräinigung vo de disjunkte Mänge $A$ und $B$
$\sqcup$	$A\sqcup B$	Disjunkti Veräinigung vo de Mänge $A$ und $B$
${}^{\mathrm {C} }$	$A^{\mathrm {C} }$	Komplemänt vo dr Mängi $A$
${\overline {~~}}$	${\overline {A}}$
${\mathcal {P}}$	${\mathcal {P}}(A)$	Potänzmängi vo dr Mängi $A$
${\mathfrak {P}}$	${\mathfrak {P}}(A)$

Mängerelazione

Sümbol	Verwändig	Interprezation
$\subset$	$A\subset B$	$A$ isch en ächti Däilmängi vo $B$
$\subsetneq$	$A\subsetneq B$
$\subseteq$	$A\subseteq B$	$A$ isch e Däilmängi vo $B$
$\supset$	$A\supset B$	$A$ isch en ächti Obermängi vo $B$
$\supsetneq$	$A\supsetneq B$
$\supseteq$	$A\supseteq B$	$A$ isch en Obermängi vo $B$
$\in$	$a\in A$	s Elimänt $a$ isch in dr Mängi $A$ enthalte
$\ni$	$A\ni a$
$\notin$	$a\notin A$	s Elimänt $a$ isch nit in dr Mängi $A$ enthalte
$\not \ni$	$A\not \ni a$

Hinwiis: d Sümbol $\subset$ und $\supset$ wärde nit äihäitlig verwändet und schliesse hüfig d Gliichhäit vo de bäide Mängene nit us.

Zaalemängene

Sümbol	Verwändig	Interpretazion
$\mathbb {N}$		natürligi Zaale
$\mathbb {Z}$		ganzi Zaale
$\mathbb {Q}$		razionali Zaale
$\mathbb {A}$		algebraischi Zaale
$\mathbb {R}$		reelli Zaale
$\mathbb {C}$		komplexi Zaale
$\mathbb {H}$		Quaternione

Mächtigkäite

Sümbol	Verwändig	Interpretazion
$|~~|$	$|A|$	Mächtigkäit (Kardinalität) von ere Mängi $A$
$\#$	$\#A$
${\mathfrak {c}}$		Mächtigkäit vom Kontinuum
$\aleph$	$\aleph _{0}$, $\aleph _{1}$, ...	Kardinalzaale
$\beth$	$\beth _{0}$, $\beth _{1}$, ...	Beth-Zaale

E baar Begriff aaschaulig gmacht

• 
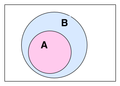
  $A$ isch en (ächti) Däiilmängi vo $B$
• 
  In root: D Schnittmängi vo $A$ und $B$
• 
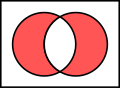
  In root: D Veräinigungsmängi vo $A$ und $B$
• 
  In root: D Differänzmängi $A$ ooni $B$
• 
  In root: Die sümmetrischi Differänz vo $A$ und $B$
• 
  In blau: S relative Komplemänt vo $A$ in $B$
• 
  In grau: s absolute Komplemänt vo $A$ im Uniwersum $U$
• 
  S kartesische Brodukt $\scriptstyle A\times B$ vo de bäide Mänge $\scriptstyle A=\{x,y,z\}$ und $\scriptstyle B=\{1,2,3\}$

Literatur

• Felix Hausdorff: Grundzüge der Mengenlehre. Chelsea Publ. Co., New York 1914/1949/1965, ISBN 978-3-540-42224-2.
• Adolf Fraenkel: Einleitung in die Mengenlehre. Springer Verlag, Berlin/Heidelberg/New York 1928. Neudruck: Martin Sändig oHG, Walluf 1972, ISBN 3-500-24960-4.
• Paul R. Halmos: Naive Mengenlehre. Vandenhoeck & Ruprecht, Göttingen 1968, ISBN 3-525-40527-8.
• Erich Kamke: Mengenlehre. 6. Auflage. Walter de Gruyter & Co., Berlin 1969.
• Kenneth Kunen: Set Theory: An Introduction to Independence Proofs. North-Holland, 1980, ISBN 0-444-85401-0.
• Arnold Oberschelp: Allgemeine Mengenlehre. Mannheim/Leipzig/Wien/Zürich 1994.
• André Joyal, Ieke Moerdijk: Algebraic Set Theory. Cambridge University Press, 1995, ISBN 0-521-55830-1.
• Heinz-Dieter Ebbinghaus: Einführung in die Mengenlehre. Spektrum Akademischer Verlag, Heidelberg/Berlin 2003, ISBN 3-8274-1411-3.

Weblingg

 Wikibooks: Mathe für Nicht-Freaks: Mengenlehre — Lern- und Lehrmaterialie
 Wikibooks: Beweisarchiv: Mengenlehre — Lern- und Lehrmaterialie