Wektor

E aglüegti Version vo derre Site, wo am 13. Jänner 2020 freige worre isch, basiert uff derre Version.

Im allgemäine Sinn verstoot mä under eme Wektor (lat. vector „Drääger, Faarer“) en Elimänt vom ene Wektorruum, das häisst en Objekt, wo zu andere Wektoren addiert cha wärde und mit Zaale, wo as Skalar bezäichnet wärde, cha multipliziert wärde. Wektore in däm allgemäine Sinn wärde im Ardikel Wektorruum behandlet.

Im ängere Sinn verstoot mä under eme Wektor

in dr analütische Geometrii e mathematischs Objekt, wo e Parallelverschiebig in dr Ebeni oder im Ruum beschribt. In kartesische Koordinate wärde Wektore dur Zaalebäärli (in dr Ebeni) bzw. Zaaletripel (im Ruum) daargstellt, wo vilmol äns under em ander (as „Spaltewektore“) gschriibe wärde.
vo dere Basis us e $n$ -Tupel vo reelle Zaale,^[1] also en Elimänt vo $\mathbb {R} ^{n}$ .
in dr klassische Füsik e füsikalischi Gröössi, wo e Betrag und e Richdig het. Für wektorielli Gröössene in dr Füsik gälte die gliiche geometrische Gsetz und Rächereegle wie für die geometrische Wektore.

Bischbil vom Rächne mit Wektore

Zwäi geometrischi Wektore zämmezrächne entspricht däm wemm mä d Verschiebige, wo zun ene ghööre, hinderenander usfüert. Geometrisch cha mä zwäi Wektor ${\vec {a}}$ und ${\vec {b}}$ addiere, wemm mä die bäide Wektor so dur Pfiil daarstellt, ass dr Startpunkt vom zwäite Pfiil uf em Ändpunkt vom erste Pfiil lit. D Summe ${\vec {a}}+{\vec {b}}$ wird denn dur e Pfiil vom Startpunkt vom erste bis zum Ändpunkt vom zwite Pfiil daargestellt.

Mä cha aber de bäide Pfiil au e gmäinsame Aafangspunkt gee und ergänzt die Figur zum ene Parallelogramm. Dr diagonali Pfiil vo däm Aafangspunkt us bis zum Egge gegenüber stellt denn d Summe vo de bäide Vektore daar. In dr Füsik brucht mä die Konstrukzion bim Chreftparallelogramm.

In Koordinate rächnet mä d Summe Komponänte um Komponänte us: Für d Summe vo de bäide Wektor

{\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}

und

{\vec {b}}={\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}

gältet

{\vec {a}}+{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}+{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}+b_{1}\\a_{2}+b_{2}\\a_{3}+b_{3}\end{pmatrix}}

.

Für d Addizion vo Wektor gälte s Assoziativ- und s Kommutativgsetz.

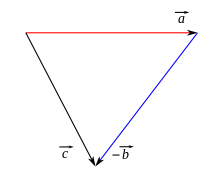
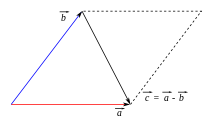
Für d Differänz vo zwäi Vektor ${\vec {a}}$ und ${\vec {b}}$ gältet:

{\vec {a}}-{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}-{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}-b_{1}\\a_{2}-b_{2}\\a_{3}-b_{3}\end{pmatrix}}

.

Litratuur

Kurt Bohner, Peter Ihlenburg, Roland Ott: Mathematik für berufliche Gymnasien – Lineare Algebra – Vektorielle Geometrie. Merkur, Rinteln 2004. ISBN 3-8120-0552-2
Klaus Jänich: Lineare Algebra. 10. Uflaag. Springer, Berlin 2004. ISBN 3-540-40207-1.
Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Band 1. 11. Uflaag, Vieweg, Wiesbade 2007, ISBN 978-3-8348-0224-8