Dräiäcksungliichung

Dialäkt: Mìlhüüserdiitsch

Ìn dr Geometrii ìsch d’ Dräiäcksungliichung a Sàtz, wo sajt, àss a Dräiäcksitta kìrzer odd’r so làng wia d’ Summa vu da baida àndra Sitta-n-ìsch.

D’ Dräiäcksungliichung schpììlt àui ìn àndra Tailgebiata vu dr Màthemàtik a wìchtiga Rolla, wia zem Biischpììl ìn dr Lineààra Àlgebra odd’r dr Funkzioonsànàlüüsa.

Bschriiwung vu dr Ungliichung

fìr àllgmaina Dräiäcka

Dreieck

Noh dr Dräiäcksungliichung ìsch ìm Dräiäck d’ Summa vu da Länga vu zwai Sitta $a$ un $b$ schtets mìndeschtens so grooss wia d’ Länga vu dr drìtta Sitta $c$:

$c\leq a+b$.

Maa kààt àui sààga, dr Àbschtànd vun A uff B ìsch klainer odd’r soo grooss wia dr Àbschtànd vun A uff C un vu C uff B zamma. Aifàcher gsajt: „Dr diräkta Waag ìsch ìmmer dr kìrzescht.“

S’ Gliichhaitszaicha gìlt numma, wänn $a$ un $b$ Tailschträcka vun $c$ sìnn – àlso wänn dr Dräiäck äntàrtet ìsch.

Waaga dr Sümmetrii hàt maa-n-àui $a\leq c+b$, un domìt $a-b\leq c$; maa hàt àui nàdììrlig $b-a\leq c$. Àlso ìnsgsàmt:

$\left|a-b\right|\leq c\leq a+b$.

D’ lìnka Ungliichung $\left|a-b\right|\leq c$ nännt maa-n-àui mànckmol umgekehrta Dräiäcksungliichung.

D’ Dräiäcksungliichung düat Àbschtànds- un Betrààgsfunkzioona kàràkterisiara. Sa wìrd àlso àls Axiom fìr àbschtràkta-n-Àbschtàndsfunkzioona ìn meetrischa Ràuima gsätzt.

fìr rachtwìnkliga Dräiäcka

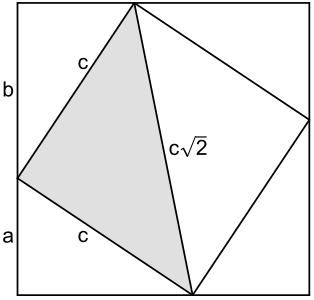
Ìsch $c$ d’ Länga vu dr Hüpothenüüsa un sìnn $a$ un $b$ d’ Kàtheetalänga vu’ma rachtwìnkliga Dräiäck, soo gìlt d’ schpeziälla Dräiäcksungliichung $a+b\leq c{\sqrt {2}}$.

• 
  wia dr Fàll vu dr Ungliichhait üsssììht
• 
  wia dr Fàll vu dr Gliichhait üsssììht

fìr reälla Zààhla

Fìr reälla Zààhla $a$ un $b$ gìlt: $|a+b|\leq |a|+|b|.$

Bewiis: Säjga $a$ un $b$ reälla Zààhla. Äntwaader ’s ìsch $a+b\geq 0$ odd’r ’s ìsch $a+b<0$. Fìr dr Fàll $a+b\geq 0$ gìlt $|a+b|=a+b$, un d’ Summa $a+b$ làsst sìch waaga $a\leq |a|$ un $b\leq |b|$ nach oben àbschätza dur $a+b\leq |a|+|b|$. Ìnsgsàmt hàt maa somìt $|a+b|\leq |a|+|b|$. Fìr dr Fàll $a+b<0$ gìlt $|a+b|=-(a+b)=-a-b$, un $-a-b$ làsst sìch waaga $-a\leq |a|$ un $-b\leq |b|$ eewafàlls dur $|a|+|b|$ nach oben àbschätza, so dàss àui ìn dam Fàll $|a+b|\leq |a|+|b|$.

d’ umgekehrta Dräiäcksungliichung

Wia biim Dräiäck kààt maa-n-àui a umgekehrta Dräiäcksungliichung harlaita

Uffgrund dr Dräiäcksungliichung gìlt $|a+b|-|b|\leq |a|.$ Wänn maa $a:=x+y,\ b:=-y$ iisätzt, nooh hàt maa

$|x|-|y|\leq |x+y|.$

Wänn maa schtàttdässa $b:=-x$ sätzt, nooh hàt maa

$|y|-|x|\leq |x+y|,$

zamma àlso (dänn fìr beliabiga reälla Zààhla $u$ und $c$ mìt $u\leq c$ un $-u\leq c$ gìt àui $|u|\leq c$)

${\Big |}|x|-|y|{\Big |}\leq |x+y|\leq |x|+|y|.$

Wänn maa $y$ dur $-y$ ärsätzt, noh ärhàlt maa-n-àui

${\Big |}|x|-|y|{\Big |}\leq |x-y|\leq |x|+|y|.$

Ìnsgsàmt àlso

${\Big |}|x|-|y|{\Big |}\leq |x\pm y|\leq |x|+|y|$ fìr àlla $x,\,y\in \mathbb {R} .$

fìr kùmpläxa Zààhla

Fìr kùmpläxa Zààhla gìlt:

$|z_{1}{}+z_{2}|\leq |z_{1}|{+}|z_{2}|.$

Bewiis:

Wial àlla Sitta nìtnegàtiiv sìnn, ìsch s’ Kwàdriara-n-a Äkwiwàlanzformung un maa ärhàlt

$z_{1}{\overline {z_{1}}}{+}z_{1}{\overline {z_{2}}}{+}{\underbrace {{\overline {z_{1}}}z_{2}} _{={\overline {z_{1}{\overline {z_{2}}}}}}}{+}z_{2}{\overline {z_{2}}}\ \leq \ z_{1}{\overline {z_{1}}}{+}2{\underbrace {|z_{1}z_{2}|} _{=|z_{1}{\overline {z_{2}}}|}}{+}z_{2}{\overline {z_{2}}},$

dr Ìwwerschtrìch bediitet doo a kùmpläxa Konjugàzioon. Wänn maa gliicha-Üssdrìck schtriicht un $z{\mathrel {:=\,}}z_{1}{\overline {z_{2}}}$ sätzt, soo blibbt

$z{+}{\bar {z}}\leq 2{|z|}$

z’ zaiga. Mìt $z=u{+}iv$ ärhàlt maa

$(u{+}iv){+}(u{-}iv)=2u\leq 2{\sqrt {u^{2}{+}v^{2}}}$

bzw.

$|u|\leq {\sqrt {u^{2}{+}v^{2}}},$

wàs waaga $0\leq v^{2}\$ un dr Monotonii vu dr (reälla) Wurzelfunkzioon ìmmer ärfìllt ìsch.

Wia biim reälla Fààl folgt üss dara Ungliichung àui

${\Big |}|z_{1}|{-}|z_{2}|{\Big |}\leq |z_{1}{\pm }z_{2}|\leq |z_{1}|{+}|z_{2}|$ fìr àlla $z_{1},\,z_{2}\in \mathbb {C} .$

vu Betrààgsfunkzioona fìr Käärwer

Zamma mìt àndra Forderunga wìrd a Betrààgsfunkzioon fìr a Käärwer $K$ àui dur d’

Dräiäcksungliichung

$\varphi (x+y)\leq \varphi (x)+\varphi (y)$

gsätzt. Sa müass fìr àlla $x,y\in K$ galta. Wänn àlla Forderunga ärfìllt sìnn, noh ìsch $\varphi$ a Betrààgsfunkzioon fìr dr Käärwer $K.$

Ìsch $\varphi (n)\leq 1$ fìr àlla gànza $n:=\underbrace {1+\dots +1} _{n{\text{-mol}}}$, nooh nännt maa dr Betrààg nìtàrkimeedisch, sunscht àrkimeedisch.

Bii nìtàrkimeedischa Betraag gìlt d’

verschärfta Dräiäcksungliichung

$\varphi (x+y)\leq \max(\varphi (x),\varphi (y)).$

Sa màcht dr Betrààg züa ainem ultràmeetrischa. Umgekehrt ìsch jeeder ultràmeetrischa Betrààg nìtàrkimeedisch.

fìr Summa un Ìntegrààla

Wämm’r mehrmols d’ Dräiäcksungliichung bzw. vollschtandiga Ìndukzioon ààwanda düat, nooh ärhàlt maa

$\left|\sum _{i=1}^{n}x_{i}\right|\leq \sum _{i=1}^{n}\left|x_{i}\right|$

fìr reälla odd’r kùumpläxa Zààhla $x_{i}\;$. Dia Ungliichung gìlt àui, wänn maa Ìntegrààla ààschtälla vu Summa betràchtet:

Ìsch $f\colon [a,b]\to \mathbb {R}$ a Riemann-ìntegriarbààra Funkzioon, nooh gìlt

$\left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx$.

Dàs gìlt àui fìr kùmpläxwaartiga Fukzioona $f\colon [a,b]\to \mathbb {C}$. Nooh gìtt’s naamlig a kùmpläxa Zààhl $\alpha$, so dàss

$\alpha \int _{a}^{b}f(x)\,dx=\left|\int _{a}^{b}f(x)\,dx\right|$ und $|\alpha |=1\;$.

Wial

$\left|\int _{a}^{b}f(x)\,dx\right|=\alpha \int _{a}^{b}f(x)\,dx=\int _{a}^{b}\alpha \,f(x)\,dx=\int _{a}^{b}\operatorname {Re} (\alpha f(x))\,dx+i\,\int _{a}^{b}\operatorname {Im} (\alpha f(x))\,dx$

reäll ìsch, müass $\int _{a}^{b}\operatorname {Im} (\alpha f(x))\,dx$ gliich Null sìì. Üsserdam gìlt

$\operatorname {Re} (\alpha f(x))\leq |\alpha f(x)|=|f(x)|$,

ìnsgsàmt àlso

$\left|\int _{a}^{b}f(x)\,dx\right|=\int _{a}^{b}\operatorname {Re} (\alpha f(x))\,dx\leq \int _{a}^{b}|f(x)|\,dx$.

fìr Wektoora

Fìr Wektoora gìlt:

$\left|{\vec {a}}+{\vec {b}}\right|\leq \left|{\vec {a}}\right|+\left|{\vec {b}}\right|$.

D’ Gìltikait vu dara Beziihung sììht maa dur Quadrieren

$\left|{\vec {a}}+{\vec {b}}\right|^{2}=\left\langle {\vec {a}}+{\vec {b}},{\vec {a}}+{\vec {b}}\right\rangle =\left|{\vec {a}}\right|^{2}+2\left\langle {\vec {a}},{\vec {b}}\right\rangle +\left|{\vec {b}}\right|^{2}\leq \left|{\vec {a}}\right|^{2}+2\left|{\vec {a}}\right|\left|{\vec {b}}\right|+\left|{\vec {b}}\right|^{2}=\left(\left|{\vec {a}}\right|+\left|{\vec {b}}\right|\right)^{2}$,

unt’r Ààwandung vu dr Cauchy-Schwarzscha Ungliichung:

$\langle {\vec {a}},{\vec {b}}\rangle \leq \left|{\vec {a}}\right|\cdot \left|{\vec {b}}\right|$.

Àui doo folgt wia-n-ìm reälla Fàll

${\Big |}\left|{\vec {a}}\right|-\left|{\vec {b}}\right|\,\,{\Big |}\leq \left|{\vec {a}}\pm {\vec {b}}\right|\leq \left|{\vec {a}}\right|+\left|{\vec {b}}\right|$

so wia

$\left|\sum _{i=1}^{n}{\vec {a}}_{i}\right|\leq \sum _{i=1}^{n}\left|{\vec {a}}_{i}\right|.$

fìr Kugeldräiäcka

zwai Kugeldräiäcka

Ìn Kugeldräiäcka gìlt d’ Dräiäcksungliichung ìm Àllgmaina nìt. Sa gìlt jedoch, wänn ma sìch uff eulerscha Dräiäcka beschrànkt, àlso salla, ìn dana jeeda Sitta kìrzer àls a hàlwer Groosskrais ìsch.

Ìn dr Àbbìldung doo dràà gìlt zwààr

$\left|a-b\right|\leq c_{1}\leq a+b,$

jedoch ìsch $c_{2}>a+b$.

fìr nomiarta Ràuima

Ìn’ma normiarta Ràuim $\left(X,\|{\cdot }\|\right)$ wìrd d’ Dräiäcksungliichung ìn dr Form

$\|x+y\|\leq \|x\|+\|y\|$

àls aina vu da Aigaschàfta gfordert, wo d’ Norm fìr àlla $x,y\in X\;$ müass ärfìlla. Bsunderscht folgt àui doo

${\Big |}\|x\|-\|y\|{\Big |}\leq \|x\pm y\|\leq \|x\|+\|y\|$

so wia

$\left\|\sum _{i=1}^{n}x_{i}\right\|\leq \sum _{i=1}^{n}\|x_{i}\|$ fìr àlla $x_{i}\in X\;$.

Ìm Schpeziààlfàll vu da L^p-Ràuima wìrd d’ Dräiäcksungliichung Minkowski-Ungliichung gnännt un mìttels dr Hölderscha Ungliichung bewììsa.

fìr meetrischa Ràuima

Ìn’ma meetrischa Ràuim $\left(X,d\right)$ wìrd àls Axiom fìr d’ àbschtàkta-n-Àbschtàndsfunkzioon verlàngt, àss d’ Dräiäcksungliichung ìn dr Form

$d(x,y)\leq d(x,z)+d(z,y)$

fìr àlla $x,y,z\in X$ ärfìllt ìsch. Ìn jeedem meetrischa Ràuim gìlt àlso per Definizioon d’ Dräiungsungliichung. Drüss làss sìch àblaita, àss ìn’ma meetrischa Ràuim àui d’ umgekehrta Dräiäcksungliichung

$\left|d(x,z)-d(z,y)\right|\leq d(x,y)$

fìr àlla $x,y,z\in X$ gìlt. Üsserdam gìlt fìr beliabiga $x_{i}\in X\;$ d’ Ungliichung

$d(x_{0},x_{n})\leq \sum _{i=1}^{n}d(x_{i-1},x_{i})$.

Lüag àui

• d’ Ungliichunga ìn Viaräcka

Lìteràtüür

• Dreiecksungleichung. In: Brockhüüs Enzüklopädii. Brockhüüs (brockhaus.de [abgerufen am 8. Oktober 2023]). 
• Triangle inequality. In: Encyclopædia Britannica. Encyclopædia Britannica, Inc. (britisches Englisch, britannica.com [abgerufen am 7. Oktober 2023]). 
• Triangle inequality. In: Paul E. Black (Hrsg.): Dictionary of Algorithms and Data Structures. National Institue of Standards and Technology, 2004 (amerikanisches Englisch, nist.gov [abgerufen am 7. Oktober 2023]). 

Weblìnks

 Commons: Dräiäcksungliichung – Sammlig vo Multimediadateie

• Eric W. Weisstein: Triangle inequality. In: MathWorld (änglisch).
• Triangle inequality. In: PlanetMath. (änglisch)

Ainzelnoohwiisa

Dä Artikel basiert uff ere fräie Übersetzig vu dere Version vum Artikel „Dreiecksungleichung“ vu de hochdütsche Wikipedia. E Liste vu de Autore un Versione isch do z finde.