Logarithmus

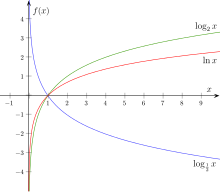
As Logarithmus (Plural: Logarithme; vo altgriechisch: λόγος, lógos, „Verständnis, Leer, Verheltnis“, und ἀριθμός, arithmós, „Zaal“) von ere (positive reelle) Zaal zur Basis bezäichnet mä d Zaal , wo d Gliichig lööst. Mä schribt . S Logarithmiere, d. h. dr Übergang vo zu , isch also en Umcheeroperazioon vom Potenziere. D Funkzioon, wo zun ere feste Basis jedere positive Zaal iire Logarithmus zueordnet, nennt mä Logarithmusfunkzioon zur Basis .
Mit Logarithme cha mä Zaaleräije, wo stark waggse, übersichtlig daarstelle, wil dr Logarithmus für groossi Zaale vil langsamer stigt as d Zaale sälber. Wie d Gliichig zäigt, cha mä dur s Logarithmiere e Multiplikazioon dur d Addizioon ersetze, wo rächnerisch vil weeniger Arbet git. Au beschriibe Logarithme mathematisch eligant vili technischi Brozäss und Fenomeen vo dr Natur wie öbbe s Verhalte von ere Halbläiter-Diode, d Spirale vom ene Schnäggehuus oder wie s menschlige Oor underschiidligi Lutsterke woornimmt.
Logarithmischi Berächnige si in Indie scho us dr Zit vor dr Zitewändi überliefert. Dr Begriff Logarithmus isch vom John Napier im früeje 17. Joorhundert brägt worde.
Litratuur[ändere | Quälltäxt bearbeite]
- Charles Naux: Histoire des Logarithmes de Neper a Euler. Tome I, II, Blanchard, Paris 1966, 1971.
- Wolfgang Walter: Analysis I. Grundwissen Mathematik Band 3. Springer, Berlin 1985, ISBN 3-540-12780-1.
- Klaus Jänich: Funktionentheorie. Eine Einführung. Springer, Berlin 2004, ISBN 3-540-20392-3.
Weblingg[ändere | Quälltäxt bearbeite]
 Wikibooks: Logarithmengesetze — Lern- und Lehrmaterialie
Wikibooks: Logarithmengesetze — Lern- und Lehrmaterialie- Eric W. Weisstein: Logarithm. In: MathWorld (änglisch).
- Logarithme
- Logarithme und Logarithmusgsetz (Onläinkurs, Üebige, Applets und Lingg)
| Dä Artikel basiert uff ere fräie Übersetzig vum Artikel „Logarithmus“ vu de dütsche Wikipedia. E Liste vu de Autore un Versione isch do z finde. |







