Kreuzprodukt

Chrüzprodukt

S Chrüzprodukt $\vec a\times\vec b$ (au Vektorprodukt, vektoriells Produkt oder üssers Produkt) vo zwei Vektore $\vec a$ und $\vec b$ im dreidimensionale reelle Vektorruum isch e Vektor, wo sänkrächt uf der Ebeni stoht, wo vo de beide Vektore ufgspannt wird und bildet mit ene e Rächtssystem. D Lengi vo däm Vektor isch d Flechegrössi vom Parallelogramm mit de Siite $\vec a$ und $\vec b$.

In der Physik wird s Chrüzprodukt zum Bispil bi der Berächnig vo der Lorentzchraft oder em Dreihmomänt bruucht: S Dreihmomänt isch Chraftarm mol Chraft

$\vec M =\vec r \times \vec F$.

Wie me gseht schribt me s Chrüzprodukt mit eme Chrüz as Multiplikationszeiche. Es isch

$\vec{a}\times\vec{b} = \left|\vec{a}\right|\, \left|\vec{b}\right|\, \sin\theta \, \vec{n}\,.$

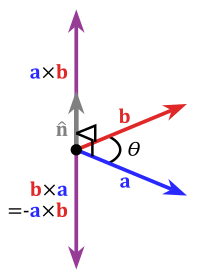
Drbii si $\vert\vec{a}\vert$ und $\vert\vec{b}\vert$ d Lengene vo de Vektore $\vec{a}$ und $\vec{b}$ und $\sin \theta \,$ isch der Sinus vom Winggel $\theta$, wo von ene igschlossen isch. Der Vektor $\vec{n}$ isch der Eiheitsvektor, wo zu $\vec{a}$ und $\vec{b}$ sänkrächt isch und wo se zum ene Rächtssystem ergänzt. Das heisst, $\vec a\,,$ $\vec b$ und $\vec{a}\times\vec{b}$ verhalte sich wie dr Duume, dr Zeigfinger und dr Mittelfinger vo der rächte Hand (Rächti-Hand-Regle).

Dr Artikel basiert uf 'ra freie Ibersetzung vum Artikel „Kreuzprodukt“ us dr dytsche Wikipedia.
E Lischte mit de dörtige Autore kasch dörte aluege