Archimedischi Körper
Die archimedische Körper si e Klass vo regelmäässige geometrische Körper. Charakteristisch für sä isch, ass mä iiri Egge nit vonenander cha underschäide. Je noch däm wie mä sä zelt, git s 13 oder 15 sonigi Körper. Si si noch em antike griechische Mathematiker Archimedes benennt, wo sä alli vermuetlig scho im dritte Joorhundert vor dr Zitewändi entdeggt het. D Schrift drüber vom Archimedes isch nit erhalte, es isch nume e Zämmefassig vom alexandrinische Mathematiker Pappos (4. Joorhundert noch dr Zitewändi) überliiferet.[1]
Die platonische Körper si e Klass vo geometrische Körper, wo no regelmäässiger si. Bi iine si au alli Fleche gliich.
Die äinzelne archimedische Körper[ändere | Quälltäxt bearbeite]
| Naame und Bild | Fleche | Kante | Egge | Folg vo de Fleche an den Egge |
Sümmetrii- gruppe |
|---|---|---|---|---|---|
Tetraederstumpf
|
8 (4 Dreiegg, 4 Säggsegg) |
18 | 12 | (3,6,6)
Dreiegg–Säggsegg–Säggsegg |
Td |
Kuboktaeder
|
14 (8 Dreiegg, 6 Kwadrat) |
24 | 12 | (3,4,3,4)
Dreiegg–Kwadrat–Dreiegg–Kwadrat |
Oh |
Hexaederstumpf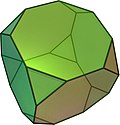
|
14 (8 Dreiegg, 6 Achtegg) |
36 | 24 | (3,8,8)
Dreiegg–Achtegg–Achtegg |
Oh |
Oktaederstumpf
|
14 (6 Kwadrat, 8 Säggsegg) |
36 | 24 | (4,6,6)
Kwadrat–Säggsegg–Säggsegg |
Oh |
(Kleines) Rhombekuboktaeder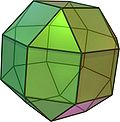
|
26 (8 Dreiegg, 18 Kwadrat) |
48 | 24 | (3,4,4,4)
Dreiegg–Kwadrat–Kwadrat–Kwadrat |
Oh |
| Groosses Rhombekuboktaeder oder Kuboktaederstumpf 
|
26 (12 Kwadrat, 8 Säggsegg, 6 Achtegg) |
72 | 48 | (4,6,8)
Keadrat–Säggsegg–Achtegg |
Oh |
Ikosidodekaeder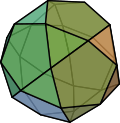
|
32 (20 Dreiegg, 12 Fümfegg) |
60 | 30 | (3,5,3,5)
Dreiegg–Fümfegg–Dreiegg–Fümfegg |
Ih |
Dodekaederstumpf
|
32 (20 Dreiegg, 12 Zääegg) |
90 | 60 | (3,10,10)
Dreiegg–Zääegg–Zääegg |
Ih |
| Ikosaederstumpf oder Fuessballkörper 
|
32 (12 Fümfegg, 20 Säggsegg) |
90 | 60 | (5,6,6)
Fümfegg–Säggsegg–Säggsegg |
Ih |
| Abgschregts Hexaeder oder Cubus simus (zwäi Variante, wo spiegelbildlig entgegegsetzt si)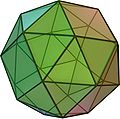  
|
38 (32 Dreiegg, 6 Kwadrat) |
60 | 24 | (3,3,3,3,4)
Dreiegg–Dreiegg–Dreiegg–Dreiegg–Kwadrat |
O |
(Chliises) Rhombeikosidodekaeder
|
62 (20 Dreiegg, 30 Kwadrat, 12 Fümfegg) |
120 | 60 | (3,4,5,4)
Dreiegg–Kwadrat–Fümfegg–Kwadrat |
Ih |
| Groosses Rhombeikosidodekaeder oder Ikosidodekaederstumpf 
|
62 (30 Kwadrat, 20 Säggsegg, 12 Zääegg) |
180 | 120 | (4,6,10)
Kwadrat–Säggsegg–Zääegg |
Ih |
| Abgschregts Dodekaeder oder Dodecaedron simum (zwäi Variante, wo spiegelbildlig entgegegsetzt si)  
|
92 (80 Dreiegg, 12 Fümfegg) |
150 | 60 | (3,3,3,3,5)
Dreiegg–Dreiegg–Dreiegg–Dreiegg–Fümfegg |
I |
Litratuur[ändere | Quälltäxt bearbeite]
- Paul Adam, Arnold Wyss: Platonische und Archimedische Körper, ihre Sternformen und polaren Gebilde. Verlag Freies Geistesleben u. a., Stuttgart 1984, ISBN 3-7725-0965-7 (2. Uflaag. Haupt u. a., Bärn 1994).
Fuessnoote[ändere | Quälltäxt bearbeite]
- ↑ Mathematicae collectiones V, 19
Weblingg[ändere | Quälltäxt bearbeite]
Commons: Archimedische Körper – Sammlig vo Multimediadateie